Projeto exploratório

de um filtro LC

Rejeita-Faixa ordem 2

na frequência de 1 kHz.



Introdução

 A atividade de caracterização de ruídos elétricos gerados naturalmente e os feitos pelo homem afetando as faixas de radio comunicação têm ganhado maior destaque dentro das atividades do Laboratório de Eletrônica visando o projeto de um sistema de antenas para as faixas de 100kHz a 30MHz para o uso local.

 A medição dos níveis de ruídos existentes serão feitas por comparações com níveis de sinais gerados localmente e iradiados por uma antena de características de radiação conhecidas, afetando a medição dos niveis de relação sinal/ruído na recepção em receptores de teste.

 Revisando a disponibilidade de instrumental suficiente para as medições pretendidas detetou-se a falta de um filtro rejeita-faixa necessário para a medição de relação sinal ruído na recepção de sinais modulados em Banda Lateral Simples ou SSB e este filtro deverá ser passivo, não demandando por alimentação externa, que pode ser fonte de interferência caso não seja criteriosamente isolada dos ruídos presentes na rêde de distribuição de energia elétrica e isto é inconveniente no presente projeto.

 Anos de vivência na área de eletrônica para telecomunicações dão a certeza de que um filtro rejeita-faixa passivo na frequência de 1 kHz para a medição de relação sinal ruído próxima de 12 dBs, usual em comunicações SSB, pode ser implementado com um circuito LC de segunda ordem com componentes existentes na sucata do laboratório a espera de um uso glorioso e assim foi feita uma busca nos componentes disponíveis.

 A busca por componentes existentes deu como resultado alguns indutores com núcleo de ferrite para uso em circuitos de voz e vários capacitores de tolerância 0,625% com dielétrico de polipropileno sabidamente de baixas perdas.

 Tendo sido localizados os componentes necessários o próximo passo foi a caracterização dos valores do componentes que será descrita a seguir.

Medição dos valores de Indutância e Fator Q de indutores.

 Os valores dos capacitores foram imediatamente identificados pois traziam impresso no corpo o valor da capacitância, já os indutores não tinham identificação alguma e para serem bem caracterizados para o uso em circuitos de filtros seletivos é necessário a determinação além do valor da indutância, os valores das perdas associadas ao enrolamento, perdas no núcleo e da frequência de auto-ressonância.

 Medidores de LCR associados a multimetros para uso normal em oficinas de reparo apenas indicam o valor da indutância medida em uma frequência que não é a esperada para o indutor. Estes instrumentos determinam bem o valor de indutância, mas para a nossa aplicação necessitamos de um instrumento a nível de laboratório que indique o valor da indutância e o valor da perda na frequência de trabalho do indutor.

 O Laboratório de Eletrônica esteve desenvolvendo um protótipo de um instrumento capaz de realizar as medições necessárias em indutores alcaçando até as frequências da faixa de VHF, mas como no momento este não está operacional para a faixa de áudio frequências, usaremos o conhecimento adquirido e improvisaremos uma montagem simplificada capaz de bom desempenho em frequências baixas.

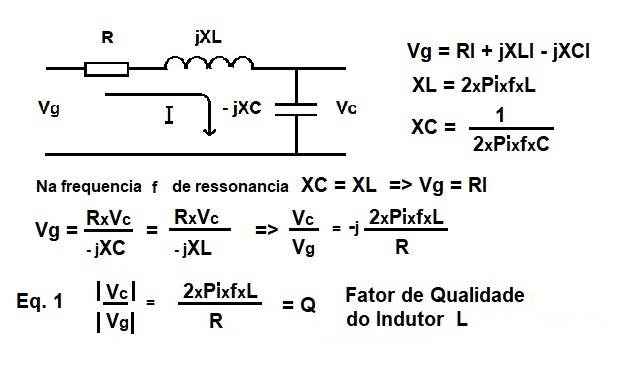  A montagem será baseada no já conhecido Circuito RLC Série em regime senoidal, velho conhecido das aulas de circuitos elétricos, mostrado na Figura 1 ao lado.

 Fazendo-se a resolução das tensões no circuito e se fizermos as seguintes considerações:

A fonte de tensão Vg é ideal com Rint = 0
O capacitor C têm perdas muito baixas.
A tensão Vc é medida por um instrumento de alta impedância de entrada.
 Chegamos sem dificuldade que a relação entre a voltagem medida nos terminais do capacitor Vc e a tensão medida nos terminais do gerador Vg é proporcional ao valor do Fator Q do indutor se considerarmos que o valor do resistor R está contido inteiramente no indutor, na forma de perdas internas.

Figura 1     Circuito RLC série.

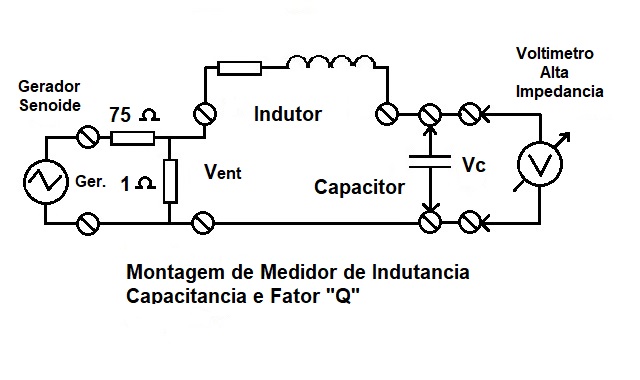
 A montagem do Medidor de Indutância e Fator Q está mostrada na Figura 2, observe que o sinal do gerador de sinais é bastante atenuado pelos resistores de 75 ohms e 1 ohms, formando um divisor de tensão com impedância de saída da ordem de 1 ohm, satisfazendo assim o requerimento de excitar o circuito RLC através de uma fonte de tensão com resistência interna bem baixa.

  O gerador de sinais de áudio deve gerar sinais senoidais com o ajuste contínuo e suave da frequência de saída. Quando se está medindo indutores com fator Q maior que 100, a sintonia e a localização do ponto de máximo torna-se bastante sensível.

  O Capacitor deve ser de boa qualidade com baixo valor de tangente do angulo de perdas, normalmente capacitores de polipropileno ou até de poliester metalizado são adequados para caracterizar indutores com o Fator Q abaixo de 100.

  Quando usar um osciloscópio como voltimetro de alta impedãncia, dê preferência em usar pontas de prova 10X de atenuação.

Figura 2     Diagrama do Medidor de Indutância e Fator Q.
  O circuito não é crítico, mas mesmo assim use conexões curtas para unir os elementos e utilize uma base de montagem estável.

 Use conectores de boa qualidade para prender os terminais do indutor e do capacitor de referência, este último terminal deve prever facilidades para a substituição do capacitor durante o processo de busca da frequência de ressonância.

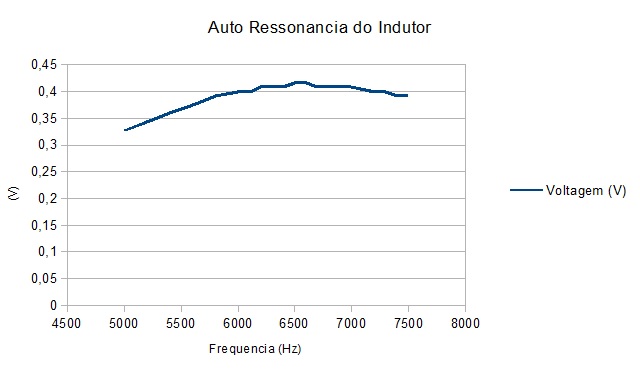
Procedimento de Ensaio de Indutores.

  O primeiro passo a ser seguido no processo de caracterização dos indutores candidatos a serem usados na implementação do Filtro Rejeita-Faixa de 1 kHz é a medida da frequência de auto-ressonância do indutor.

 Não adianta muito tentarmos usar um indutor em uma determinada frequência se a sua frequência de auto-ressonância está abaixo desta frequência, este indutor estará se comportando como um capacitor.

Figura 3     Medida da frequência de auto-ressonância do indutor.
  A montagem para a medida da frequência de auto-ressonância é a mostrada na Figura 3, o valor de R1, 100k ohms é adequado para indutâncias próximas de 2 henries.

Figura 4     Medida da frequência de auto-ressonância do indutor.
 O pico de tensão ocorre na frequência de auto-ressonância do indutor, para o indutor escolhido está por volta de 6,6 kHz.

 Ótimo, a frequência de auto-ressonância está suficientemente afastada da frequência de trabalho do indutor no filtro.

  O indutor foi montado no Medidor de Indutância e Fator Q mostrado na Figura 2.

  O valor do Capacitor foi escolhido inicialmente como 10.000 pF, valor típico utilizado em filtragem na frequência de 1 kHz.

  A frequência do Gerador foi ajustada em 1 kHz e o valor da tensão Vent foi ajustado em 10 mV.

=================================================================
Ajuste Vent para o menor valor possível, a tensão Vc pode assumir valores elevados.
==================================================================

  Ajuste a frequência do Gerador e localize a frequência de ressonância observando a tensão Vc nos terminais do capacitor.

  O valor de Indutância é dado pelo conhecida expressão de ressonância do circuito LC:

    L = 1/((2xPIxfr)x(2xPIxfr)xC)     fr (Hertz),  L (Henry)  e  C (Faraday)

Figura 5   Voltagem Vc sobre o Capacitor durante a sintonia do Medidor de Indutância e Fator Q.

  Na frequência fr = 1193 Hz  e  C = 10 nF obtêm-se o valor de Indutância L = 1,78 H

  Aplicando as voltagens Vent = 0,01 V e Vc = 0,57 V na Equaçâo 1 da Figura 1 nos dá o valor do Fator Q = 57.

  Usando-se o Medidor de Indutância e Fator Q pode-se avaliar as perdas de diferentes tipos de capacitores.

 Na Figura 6 ao lado têm-se 5 capacitores de 10 nF e os valores do Fator Q do indutor medido:

1) Capacitor cerâmico dielétrico X5U, Q medido 24

2) Capacitor Filme Poliester Metalizado, Q medido 48

3) Capacitor Filme Poliester Metalizado, Q medido 48

4) Capacitor Filme Poliester Metalizado, Q medido 48

5) Capacitor precisão Filme Polipropileno, Q medido 57

Figura 6     Diferentes tipos de capacitor.

  O circuito do Medidor de Indutância e Fator Q sempre indica de forma segura, quando afastado da frequência de auto-ressonância do indutor, o maior valor da tensão Vc que corresponde as menores perdas tanto no Indutor como no Capacitor.

  Fazendo uso da propriedade acima, é sempre possível selecionar o melhor capacitor e indutor para determinada frequência de trabalho, apenas buscando o maior valor do Fator Q através da seleção de família de capacitor e construção de indutores, diâmetro de fio, fator de forma e material magnético do núcleo.

Projeto do Filtro Rejeita-Faixa.

  No capítulo anterior fizemos a seleção e caracterização do Indutor e Capacitor com as características mais adequadas a implementação de um Filtro Rejeita-Faixa na frequência de 1kHz.

  O próximo passo agora é a determinação do valor mínimo de atenuação na faixa de passagem do filtro para possibilitar a medição do valor de 12 dB de SINAD na saída de áudio do receptor ensaiado.

  S = potência do sinal     N = potência do ruído    D = Produtos de distorções   K = fator de atenuação

  12 dB SINAD é igual a:

 (S + N + D) / (N + D)= 16   Considerando Distorções baixas < 10% , D = 0   =>  S + N = 16N  =>  S = 15N

  Atenuar S para:

  S + N = (1,1)xN   para uma incerteza menor que 1 dB.

  (15N)xK + N = (1,1)xN

  15xK + 1 = 1,1

  K = (0,1) / 15 = 0,00666

  Fazendo-se o logaritmo de K, relação de potências  =>  Atenuação = 10xLOG(0,00666) = - 21,7 dB

  O Filtro Rejeita-Faixa deverá rejeitar a frequência de 1 kHz no mínimo em 22 dB para permitir a medição do valor de SINAD de 12 dB com incerteza menor que 1 dB.
  O fator Q do indutor foi medido na frequência de 1193 Hz, bem próxima de 1000 Hz, manteremos o valor medido de Q = 57.

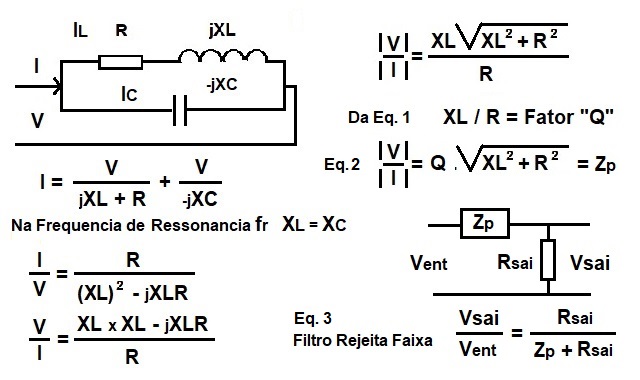
Figura 7   Circuito LC paralelo com Q finito e expressão do Filtro Rejeita-Faixa.

  Falta determinar qual o valor mínimo do Fator Q para se obter a atenuação necessária na frequência central do Filtro Rejeita-Faixa.

  Usando-se a Eq. 3 da Figura 7, que representa a estrutura do filtro a ser implementado e considerando a atenuação de 22 dB:

 (Vsai / Vent) = 10E(-22/20)   =>  (Vsai / Vent) = 0,079

  Adotando-se o valor de 10 k ohms para o Resistor Rsai, um valor que não é muito baixo ou alto para saídas de áudio comuns.

  Zp = ((1 - 0,079)xRsai) / 0,079   =>  Zp = 116,6 k ohms

  Usando a Eq. 2 da Figura 7 e fazendo-se a aproximação que Zp = Q x 2xPIxfrxL para Fator Q > 5, obtêm-se :

  Q = Zp / (2xPIxfrxL)   =>  Q = 116.600 / (6,283x1193x1,78)

  Q = 8,74   valor bem abaixo do indutor já medido que apresentou Fator Q de 57.

Cálculo dos Componentes do Filtro Rejeita_Faixa

  Já dispomos de todos os elementos necessários ao projeto do Filtro Rejeita-Faixa:
- Indutor de 1,78 H com Fator Q de 57.
- Capacitor com baixo Fator de Dissipação D e capacitância próxima de 10 nF.
- Estimativa de resistência de carga do Filtro, 10 k ohm.

  Valores dos componentes calculados em torno do valor adotado para o indutor de 1,78 H.

  Na frequência de corte fc = 1000 Hz   a Reatância XL = Rsai,  =>   Rsai = 2xPIxfcxL = 11.183 ohm.

  Na frequência de corte fc = 1000 Hz   a Reatância XL = XC,  =>   C = 1 / (2xPIxfcxRsai) = 14.231 pF.

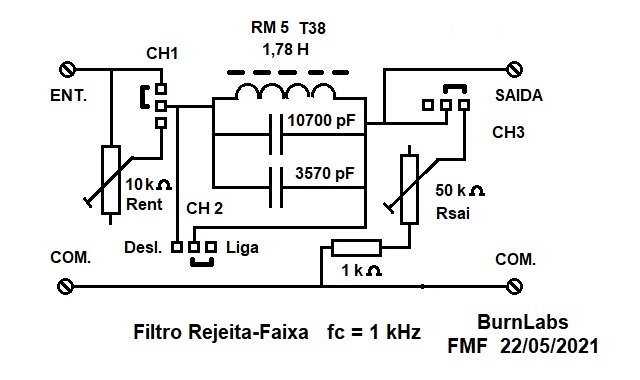Figura 8   Circuito do Filtro Rejeita-Faixa.

 O cálculo dos elementos de um filtro com apenas um elemento ressonante é bem simples, como pode ser visto acima, caso o filtro fosse de ordem acima de 2 há um acoplamento entre os diversos circuitos ressonantes em função da frequência e o cálculo é bem mais complexo.

  Caso o leitor tenha interesse em conhecer o projeto de filtros LC mais elaborados, existe bastante literatura a respeito, procure por " Sintese de Filtros LC ", "Síntese de rede" ou "Network synthesis" onde esse assunto é tratado com análise matemática bem elaborada e o uso de técnicas computacionais de cálculo numérico para se obter a estrutura e componentes do filtro para atender as curvas de resposta em frequência definidas pelo projetista.

Características do Filtro Rejeita-Faixa implementado

  O Filtro Rejeita-Faixa de ordem 2 foi calculado e implementado com componentes criteriosamente selecionados e apresentou resultados práticos bem próximos dos valores esperados.

Figura 9   Protótipo do Filtro Rejeita-Faixa 1kHz montado em placa de CI padrão.

  As Figuras 10 até a Figura 14 mostram as curvas de resposta em frequência do filtro implementado.

 Para cada curva de resposta em frequência é mostrado o valor esperado de atenuação na frequência de ressonância calculado através da Equação Eq.3 da Figura 7 e no final há um comentário a respeito dos resultados práticos e os calculados.

Figura 10   Filtro Rejeita-Faixa 1kHz, resposta ampla.

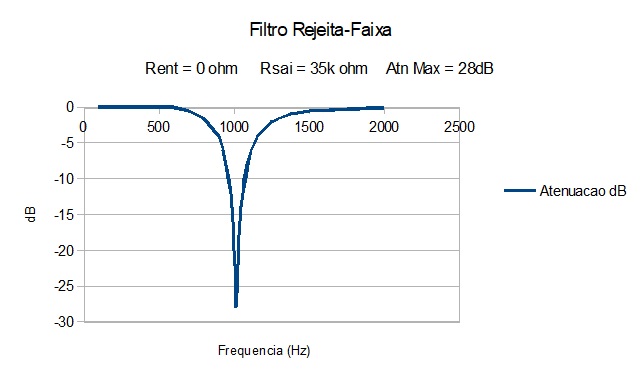
Figura 11   Filtro Rejeita-Faixa 1kHz, menor carga de saída.

  Atenuação calculada Eq.3:  Zp = 2xPIxfcxLxQ = 637.413 ohms   =>  Atn = 35.000 / (637.413 + 35.000)   = -25,7 dB.

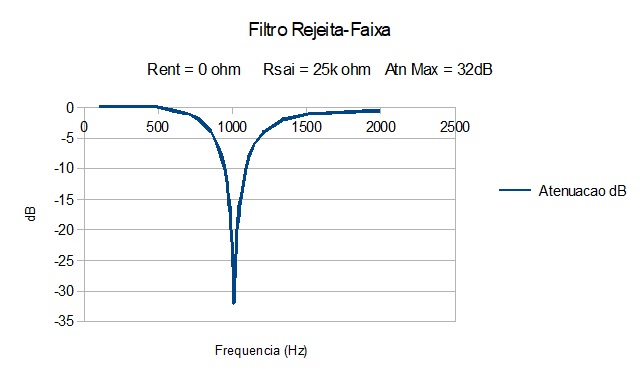
Figura 12   Filtro Rejeita-Faixa 1kHz, carga intermediaria na saída.

  Atenuação calculada Eq.3:  Zp = 2xPIxfcxLxQ = 637.413 ohms   =>  Atn = 25.000 / (637.413 + 25.000)   = -28,5 dB.

Figura 13   Filtro Rejeita-Faixa 1kHz, maior carga na saída.

  Atenuação calculada Eq.3:  Zp = 2xPIxfcxLxQ = 637.413 ohms   =>  Atn = 10.000 / (637.413 + 10.000)   = -36,2 dB.

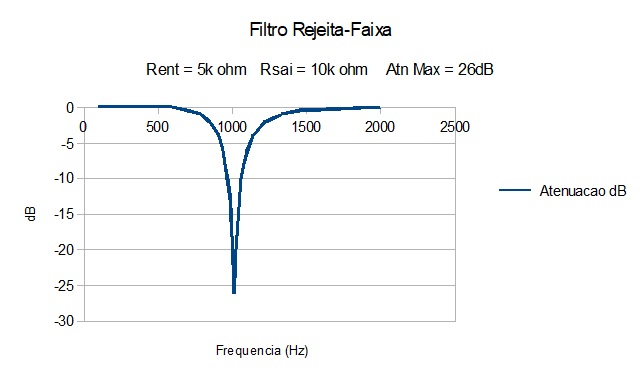
Figura 14   Filtro Rejeita-Faixa 1kHz, maior resistência da fonte.

Considerações finais

  Os valores práticos apresentaram resultados um pouco melhores que os esperados, 3,5 dB no máximo, mostrando que o valor real do fator Q do indutor é um pouco acima do medido, resultado coerente com o carregamento extra colocado no circuito RLC série pela carga da ponta de prova do osciloscópio usado para medir a voltagem no capacitor e determinação de seu Fator Q.